引言 - 二叉树是什么
在计算机科学中, 二叉树(Binary tree) 是每个结点最多只有两个分支(即不存在分支度大于2的结点)的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序,不能随意颠倒。 与普通树不同,普通树的结点个数至少为1,而二叉树的结点个数可以为0;普通树结点的最大分支度没有限制,而二叉树结点的最大分支度为2;普通树的结点无左、右次序之分,而二叉树的结点有左、右次序之分。 ——From 中文维基百科·二叉树
二叉树是非常重要的数据结构,其独特的结构使得它在搜索和处理数据方面有相当不错的表现
二叉树的遍历
层次遍历(宽度优先遍历)
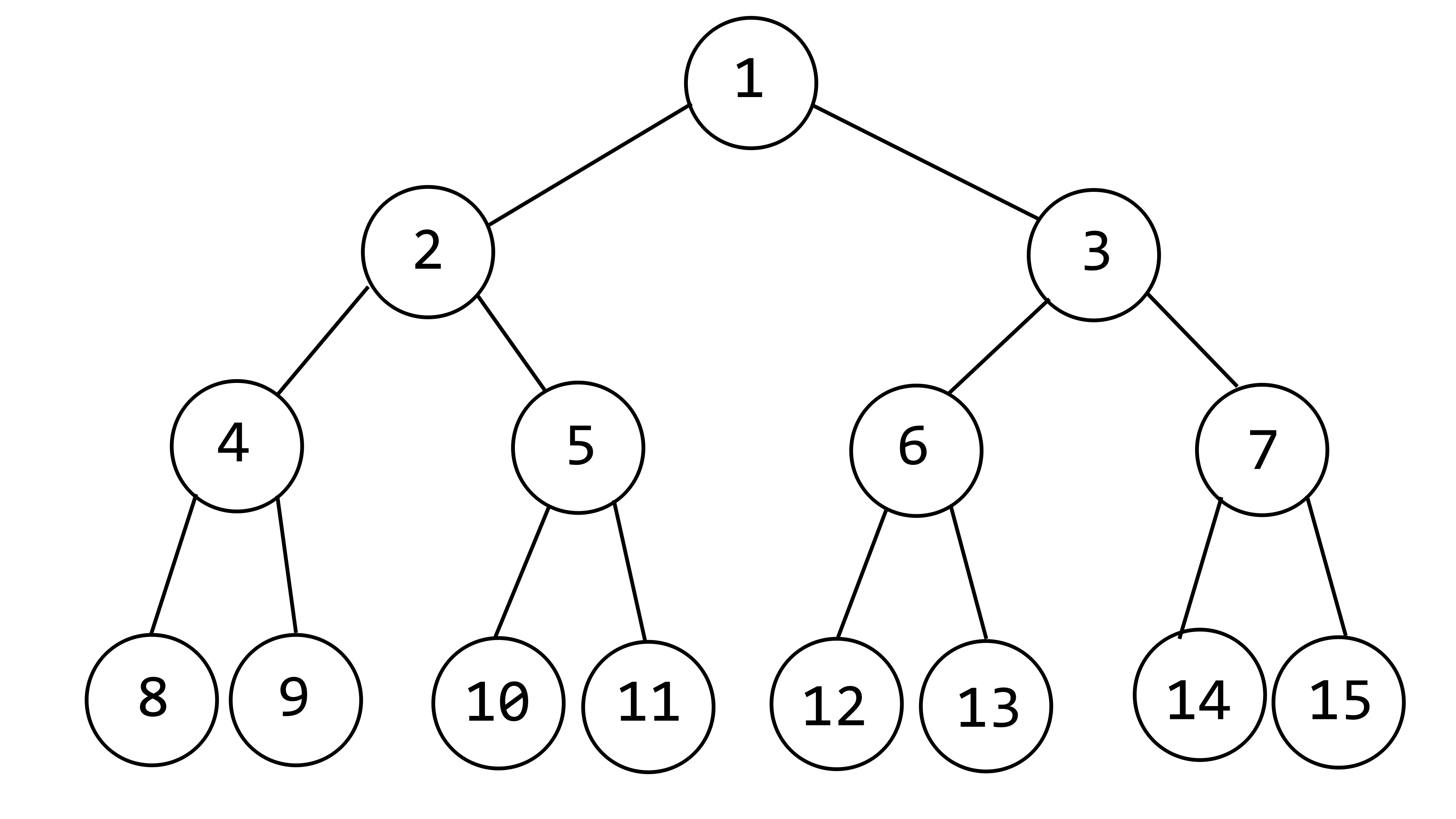
顾名思义,即按从上到下、从左到右的顺序遍历结点
以上图为例,遍历的顺序为1~15
这种方法叫 宽度优先遍历(Breadth-First Search, BFS)
递归遍历(深度优先遍历)
博主认为二叉树的递归遍历是最为精彩的部分。理解其三种递归遍历方式,能一窥二叉树的结构之美
对于一棵二叉树 T ,可以递归定义它的先序遍历、中序遍历和后序遍历,如下所示:
- PreOrder(T) = T的根结点 + PreOrder(T的左子树) + PreOrder(T的右子树)
- InOrder(T) = InOrder(T的左子树) + T的根结点 + InOrder(T的右结点)
- PostOrder(T) = PostOrder(T的左子树) + PostOrder(T的右子树) + T的根结点 这三种遍历都属于递归遍历,或者说 深度优先遍历(Depth-First Search, DFS) ,因为它总是优先往深处访问 ——From 刘汝佳《算法竞赛入门经典(第2版)》
还是以上图为例,来讲一下如何递归遍历:
要遍历整棵二叉树,首先把1,2,3看作一棵小二叉树来遍历,其中1为根,2,3为结点。遍历结点2或3时,再分别把2,4,5或3,6,7看作小二叉树来遍历,依次类推。具体遍历顺序由遍历的方式而定
是不是很简单?在看下面的答案前,先试着写一下这三种遍历方式的顺序吧
注:“根”——根结点,“左”——左子树,“右”——右子树 还是上图的例子:
先序遍历
顺序:根-->左-->右
1 2 4 8 9 5 10 11 3 6 12 13 7 14 15
中序遍历
顺序:左-->根-->右
8 4 9 2 10 5 11 1 12 6 13 3 14 7 15
后序遍历
顺序:左-->右-->根
8 9 4 10 11 5 2 12 13 6 14 15 7 3 1
实例:推导先序遍历
已知二叉树的中序遍历和后续遍历,如何推出这棵二叉树,以写出它的先序遍历?
用Python风格伪代码来表示,[]代表列表(有序),{}代表集合(无序)
InOrder = [7, 8, 11, 3, 5, 16, 12, 18]
PostOrder = [8, 3, 11, 7, 16, 18, 12, 5]
由后序遍历的特点可知,最后一个字符5就是根,在中序遍历中找到5,把{7, 8, 11, 3}看作左子树,{16, 12, 18}看作右子树,构建一棵二叉树:
5
/ \
{7, 8, 11, 3} {16, 12, 18}
接着再来看后序遍历,分别在[8, 3, 11, 7] , [16, 18, 12]中找出根,同理分别构建小二叉树:
5
/ \
7 12
\ / \
{8, 11, 3} 16 18
最后一步:
5
/ \
7 12
\ / \
11 16 18
/\
8 3
于是我们可以得到它的先序遍历:
PreOrder = [5, 7, 11, 8, 3, 12, 16, 18]
几道例题
推导先序遍历
pre_order.py
pre_order, in_order, post_order = [], '', ''
def read_list():
global pre_order, in_order, post_order
in_order = input()
post_order = input()
pre_order = []
in_order = list(map(int, in_order.split()))
post_order = list(map(int, post_order.split()))
def build_pre(in_order, post_order):
"""递归构建二叉树的先序遍历"""
global pre_order
# 直观地看到递归的步骤
print("in_order = ", in_order)
print("post_order = ", post_order)
print("pre_order = ", pre_order, "\n")
root = post_order[-1]
pre_order.append(root) # 所谓先序遍历,只需在构建子树时记录下根节点即可
root_in_order = in_order.index(root)
in_left = in_order[:root_in_order]
in_right = in_order[root_in_order+1 : len(in_order)]
post_left = post_order[:len(in_left)]
post_right = post_order[len(in_left) : -1]
if len(post_left):
build_pre(in_left, post_left)
if len(post_right):
build_pre(in_right, post_right)
while 1:
try:
read_list()
except:
break
build_pre(in_order, post_order)
print("PreOrder: ", end='')
for i in pre_order:
print(i, end=' ')
print("\n")
输出示例:
7 8 11 3 5 16 12 18 # 中序遍历
8 3 11 7 16 18 12 5 # 后序遍历
in_order = [7, 8, 11, 3, 5, 16, 12, 18]
post_order = [8, 3, 11, 7, 16, 18, 12, 5]
pre_order = [] # 读入数据
in_order = [7, 8, 11, 3]
post_order = [8, 3, 11, 7]
pre_order = [5] # 递归第一步,添加根节点5
in_order = [8, 11, 3]
post_order = [8, 3, 11]
pre_order = [5, 7] # 递归第二步,添加根节点7
in_order = [8]
post_order = [8]
pre_order = [5, 7, 11]
in_order = [3]
post_order = [3]
pre_order = [5, 7, 11, 8]
in_order = [16, 12, 18]
post_order = [16, 18, 12]
pre_order = [5, 7, 11, 8, 3]
in_order = [16]
post_order = [16]
pre_order = [5, 7, 11, 8, 3, 12]
in_order = [18]
post_order = [18]
pre_order = [5, 7, 11, 8, 3, 12, 16]
PreOrder: 5 7 11 8 3 12 16 18
树的层次遍历(Trees on the level, UVa 122)
题目:
分析:采用动态结构建树。代码出自紫书:
trees_on_the_level.cpp
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int maxn = 256 + 10;
// 节点类型
struct Node
{
bool have_value;
int v; // 节点值
Node *left, *right;
Node() : have_value(false), left(NULL), right(NULL){} // 构造函数
};
Node *root; // 二叉树的根节点
Node *newnode() { return new Node(); }
bool failed;
void addnode(int v, char *s)
{
int n = strlen(s);
Node *u = root; // 从根节点往下走
for (int i = 0; i < n; i++)
{
if (s[i] == 'L')
{
if (u->left == NULL) u->left = newnode(); // 节点不存在,建立新节点
u = u->left; // 往右走
}
else if (s[i] == 'R')
{
if (u->right == NULL) u->right = newnode();
u = u->right;
}
}
if (u->have_value) failed = true;
u->v = v;
u->have_value = true; // 别忘了做标记
}
void remove_tree(Node *u)
{
if (u == NULL) return; // 提前判断比较稳妥
remove_tree(u->left); // 递归释放左子树空间
remove_tree(u->right); // 递归释放右子树空间
delete u; // 调用u的析构函数并释放u节点本身的内存
}
char s[maxn];
bool read_input()
{
failed = false;
remove_tree(root); // 释放上一棵二叉树的内存
root = newnode();
for (;;)
{
if (scanf("%s", s) != 1) return false;
if (!strcmp(s, "()")) break;
int v;
sscanf(&s[1], "%d", &v);
addnode(v, strchr(s, ',') + 1);
}
return true;
}
bool bfs(vector<int> &ans) // 宽度优先遍历(Breadth-First Search, BFS)
{
queue<Node*> q;
ans.clear();
q.push(root); // 初始时只有一个根节点
while (!q.empty())
{
Node *u = q.front(); q.pop();
if(!u->have_value) return false; // 有节点没有被赋值过,表明输入有误
ans.push_back(u->v); // 增加到输出序列尾部
if (u->left != NULL) q.push(u->left); // 把左子节点(如果有)放进队列
if (u->right != NULL) q.push(u->right); // 把右子节点(如果有)放进队列
}
return true; // 输入正确
}
int main() {
vector<int> ans;
while(read_input())
{
if(!bfs(ans)) failed = 1;
if(failed) printf("not complete\n");
else
{
for(int i = 0; i < ans.size(); i++)
{
if(i != 0) printf(" ");
printf("%d", ans[i]);
}
printf("\n");
}
}
return 0;
}
小结:用结构体 + 指针实现二叉树。当然也可以用数组 + 下标来实现,但仍需具体情况具体分析
二叉树的递归遍历(Trees, UVa548)
题目:
分析:即已知二叉树的中序遍历和后序遍历,推出先序遍历。还是紫书:
trees.cpp
#include <iostream>
#include <string>
#include <sstream>
#include <algorithm>
using namespace std;
const int maxv = 10000 + 10;
int in_order[maxv], post_order[maxv], lch[maxv], rch[maxv];
int n;
// 因为各个结点的权值各不相同且都是正整数,直接用权值作为结点编号
bool read_list(int *a)
{
string line;
if (!getline(cin, line)) return false;
stringstream ss(line);
n = 0;
int x;
while (ss >> x) a[n++] = x;
return n > 0;
}
// 把in_order[L1..R1]和post_order[L2..R2]建成一棵二叉树,返回树根
int build(int L1, int R1, int L2, int R2)
{
if (L1 > R1) return 0; // 空树
int root = post_order[R2];
int p = L1;
while (in_order[p] != root) p++;
int cnt = p - L1; // 左子树的结点个数
lch[root] = build(L1, p-1, L2, L2+cnt-1);
rch[root] = build(p+1, R1, L2+cnt, R2-1);
return root;
}
int best, best_sum; // 目前为止的最优解和对应的权和
void dfs(int u, int sum) // Deep First Search
{
sum += u;
if (!lch[u] && !rch[u]) // 叶子
{
if (sum < best_sum || (sum == best_sum && u < best))
{
{ best = u; best_sum = sum; }
}
if (lch[u]) dfs(lch[u], sum);
if (rch[u]) dfs(rch[u], sum);
}
}
int main()
{
while (read_list(in_order))
{
read_list(post_order);
build(0, n-1, 0, n-1);
best_sum = 1000000000;
dfs(post_order[n-1], 0);
cout << best << "\n";
}
return 0;
}
小结:难点在于理解利用数组lch和rch来储存节点的左右子树以及建树的过程。
建议自己画一下示意图帮助理解
天平(Not so Mobile, UVa 839)
题目: PDF 分析:递归定义二叉树。还是紫书,代码相当精简、巧妙,值得一学:
not_so_mobile.cpp
#include <iostream>
using namespace std;
// 输入一个子天平,返回子天平是否平衡,参数W修改为子天平的总重量
bool solve(int &W)
{
int W1, D1, W2, D2;
bool b1 = true, b2 = true;
cin >> W1 >> D1 >> W2 >> D2;
if (!W1) b1 = solve(W1);
if (!W2) b2 = solve(W2);
W = W1 + W2;
return b1 && b2 && (W1 * D1 == W2 * D2); // b1:左 b2:右
}
int main()
{
int T, W;
cin >> T;
while (T--)
{
if (solve(W)) cout << "YES\n"; else cout << "NO\n";
if (T) cout << "\n";
}
return 0;
}
not_so_mobile.py
def solve(W):
b1, b2 = True, True
W1, D1, W2, D2 = map(int, input().split())
if W1 == 0:
b1 = solve(W1)
if W2 == 0:
b2 = solve(W2)
W = W1 + W2
return b1 and b2 and (W1*D1 == W2*D2)
W = 0
T = int(input())
while T > 0:
T -= 1
print("YES") if solve(W) else print("No")
if T: print("\n")
似乎翻译成 Python 后可读性更强(
Python类实现二叉树
面向对象真的很有意思,从无到有搓出一个功能完善的类 ,其兴奋感不亚于在mc中造出一台生电机器(
tree.py
class Node(object):
"""节点类"""
def __init__(self, data=None, left_child=None, right_child=None):
self.data = data
self.left_child = left_child
self.right_child = right_child
class Tree(object):
def __init__(self):
self.root = Node()
def rec_pre_order(self, node=None):
"""递归实现前序遍历"""
if node:
print(node.data, end=" ")
self.rec_pre_order(node.left_child)
self.rec_pre_order(node.right_child)
def pre_order(self):
"""非递归实现前序遍历"""
if self.root:
ls = [self.root]
while ls:
node = ls.pop()
print(node.data, end=" ")
if node.right_child:
ls.append(node.right_child)
if node.left_child:
ls.append(node.left_child)
def pre_order2(self):
"""非递归实现前序遍历"""
stack = []
node = self.root
while node or stack:
while node:
print(node.data, end=" ")
stack.append(node)
node = node.left_child
if stack:
node = stack.pop()
node = node.right_child
def rec_in_order(self, node):
"""递归实现中序遍历"""
if node:
self.rec_in_order(node.left_child)
print(node.data, end=" ")
self.rec_in_order(node.right_child)
def in_order(self):
"""非递归实现中序遍历"""
ls = []
node = self.root
while node or len(ls):
while node:
ls.append(node)
node = node.left_child
if len(ls):
node = ls.pop()
print(node.data, end=" ")
node = node.right_child
def in_order2(self):
"""非递归实现中序遍历"""
stack = []
node = self.root
while node:
while node:
if node.right_child:
stack.append(node.right_child)
stack.append(node)
node = node.left_child
node = stack.pop()
while stack and (not node.right_child):
print(node.data, end=" ")
node = stack.pop()
print(node.data, end=" ")
if stack:
node = stack.pop()
else:
node = None
def rec_post_order(self, node):
"""递归实现后序遍历"""
if node:
self.rec_post_order(node.left_child)
self.rec_post_order(node.right_child)
print(node.data, end=" ")
def post_order(self, node):
"""非递归实现后序遍历"""
q = node
ls = []
while node:
while node.left_child:
ls.append(node)
node = node.left_child
while node and (node.right_child is None or node.right_child == q):
print(node.data, end=" ")
q = node
if not ls:
return
node = ls.pop()
ls.append(node)
node = node.right_child
def get_depth(self):
"""计算树的深度,递归树的左右节点,取值大的深度"""
def _depth(node):
if not node:
return 0
else:
left_depth = _depth(node.left_child)
right_depth = _depth(node.right_child)
if left_depth > right_depth:
return left_depth + 1
else:
return right_depth + 1
return _depth(self.root)
def get_leaves(self, node):
"""递归输出所有叶子节点"""
if node:
if not node.left_child and not node.right_child:
print(node.data, end=" ")
else:
self.get_leaves(node.left_child)
self.get_leaves(node.right_child)
if __name__ == '__main__':
tree = Tree()
tree.root = Node('A')
tree.root.left_child = Node('B')
tree.root.right_child = Node('C')
tree.root.left_child.left_child = Node('D')
tree.root.left_child.right_child = Node('E')
tree.root.left_child.right_child.right_child = Node('F')
tree.root.left_child.left_child.right_child = Node('G')
print("""
A
|
-------------
| |
B C
|
-------------
| |
D E
| |
------- -------
| | | |
(None) G (None) F
""")
print("#先序遍历")
print("递归:")
tree.rec_pre_order(tree.root)
print("\n非递归1:")
tree.pre_order()
print("\n非递归2:")
tree.pre_order2()
print("\n\n#中序遍历")
print("递归:")
tree.rec_in_order(tree.root)
print("\n非递归1:")
tree.in_order()
print("\n非递归2:")
tree.in_order2()
print("\n\n#后序遍历")
print("递归:")
tree.rec_post_order(tree.root)
print("\n非递归:")
tree.post_order(tree.root)
print("\n\n二叉树的深度为:", tree.get_depth())
print("\n叶子节点:", end="")
tree.get_leaves(tree.root)
二叉查找树
(先挖个坑,以后回来更新)

参考文献
- 中文维基百科·二叉树
- 刘汝佳《算法竞赛入门经典(第2版)