Tower of Hanoi for C Language Beginners

AI Translated from Chinese

Introduction

In India, there is an ancient legend. In the temple of Benares, at the center of the world, a brass plate holds three diamond needles. When the Hindu god Brahma was creating the world, he threaded 64 gold discs from large to small onto one of the needles from bottom to top. This is the so-called Tower of Hanoi. Day and night, a monk constantly moves these gold discs to another needle according to the following rules: Only one disc can be moved at a time, and a smaller disc must always be on top of a larger one. When all the gold discs have been moved from the needle where Brahma threaded them to the third needle, the world will be destroyed in a thunderclap, and the tower, temple, and all living beings will perish together…

Problem Analysis

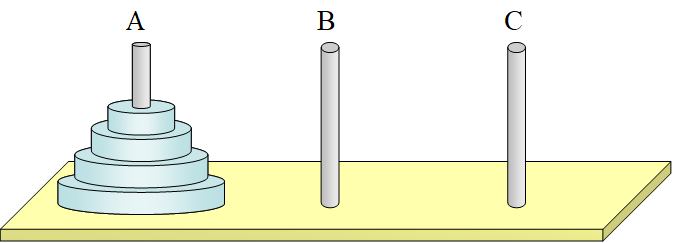
What is Tower of Hanoi

To summarize: There are three poles: A, B, and C. Pole A has n (n > 1) gold discs, with sizes decreasing from bottom to top. Only one gold disc can be moved at a time, and a larger disc cannot be placed on top of a smaller one, so that all discs are moved to pole C. Question: How to move? What is the minimum number of moves?

A Simplest Example

When n = 1, it can be solved in just 1 step: A-->C (A–>C means moving the top disc from pole A to pole C, same below)

A Very Simple Example

When n = 2, it takes just 3 steps:

A-->B
A-->C
B-->C

A Simple Example

When n = 3, solve it with a diagram:

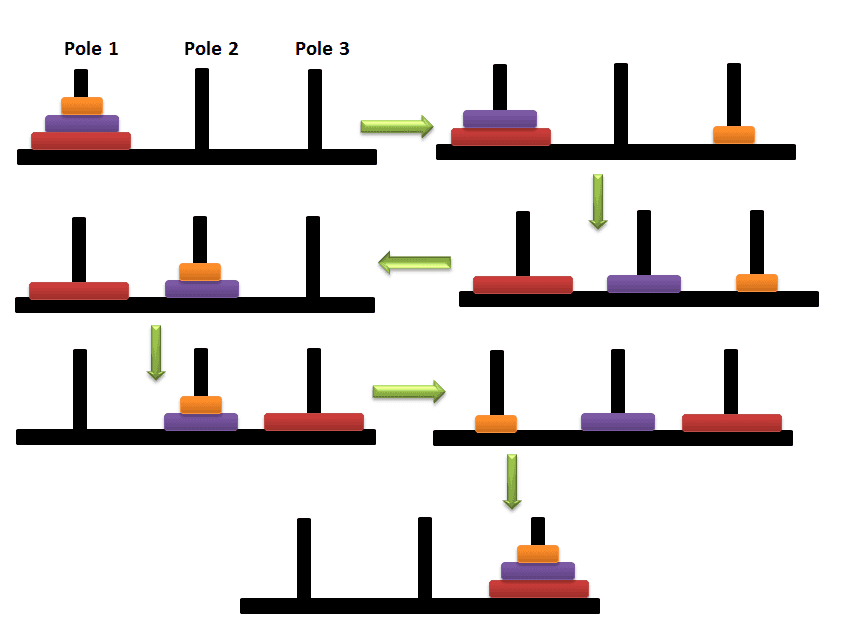
Described in words:

A-->C
A-->B
C-->B
A-->C
B-->A
B-->C
A-->C

Total of 7 steps

Extending to n

What about when n = 4, 5, 6, or even 20? This problem seems complex, but there is actually a pattern. According to mathematical calculations, the number of moves required to move an n-layer Tower of Hanoi is $2^n - 1$.

Discussion of specific proof is beyond the scope of this article.

Algorithm Analysis

The problem can be solved using recursion. Moving n discs from pole A to pole C can be decomposed into the following three steps:

• First, move the n-1 discs on pole A to pole B using C as an intermediate pole
  • This step can be further decomposed into three steps:
    • Move the n-2 discs on pole A to pole C using B as an intermediate pole
    • Move the (n-1)th disc on pole A to pole B
    • Move the n-2 discs on pole C to pole B using A as an intermediate pole
• Then move the last disc on pole A to pole C
• Finally, move the n-1 discs on pole B to pole C using A as an intermediate pole

Does it feel a bit recursive? The blogger has been learning C language recently, so I tried to implement this algorithm in C. The code is as follows.

Code

C

# include <stdio.h>
/* Tower of Hanoi problem: input the number of discs n, output the process of moving n discs from pole A (using pole B) to pole C */
int counter = 0;  /* Initialize counter */

void move(char x, char y)
/* Output one move */
{
printf("\n%c-->%c", x, y);
counter++;
}

void hanoi(int n, char one, char two, char three)
/* Recursive algorithm for Tower of Hanoi */
{
    if (n == 1)
    {
        move(one, three);
    }
    else
    {
        hanoi(n-1, one, three, two);
        move(one, three);  /* Use two as intermediate pole */
        hanoi(n-1, two, one, three);
    }
}

int main()
{
    for(;;)  /* Implement multiple simulations */
    {
        int n;
        printf("Tower of Hanoi layers: ");
        scanf("%d", &n);
        hanoi(n, 'A', 'B', 'C');
        printf("\n\nNumber of moves: %d\n\n", counter);
        counter = 0;  /* Reset counter */
    }
}

Python

Of course, Python is also included.

# Tower of Hanoi problem: input the number of discs n, output the process of moving n discs from pole A (using pole B) to pole C
counter = 0  # Initialize counter

def move(x, y):
    '''Output one move'''
    global counter
    print(f"{x}-->{y}")
    counter += 1

def hanoi(n, one, two, three):
    '''Recursive algorithm for Tower of Hanoi'''
    if n == 1:
        move(one, three)
    else:
        hanoi(n-1, one, three, two)
        move(one, three)
        hanoi(n-1, two, one, three)

while 1:
    n = int(input("Tower of Hanoi layers: "))
    hanoi(n, 'A', 'B', 'C')
    print(f"Number of moves: {counter}\n")
    counter = 0  # Reset counter

Conclusion

Reminds me of a famous quote:

Algorithm + Data Structure = Program

This is the first time the blogger seriously studied algorithms, and it opened the door to a new world (lol).

References

1. Yu Yan. C Language Programming and Practice [M]. Beijing: Tsinghua University Press, 2018 (reprinted 2019)