AI Translated from Chinese
Introduction - What is a Binary Tree
In computer science, a binary tree is a tree data structure in which each node has at most two children (i.e., there is no node with degree greater than 2). These children are typically called “left subtree” or “right subtree.” The branches of a binary tree have left-right order and cannot be reversed arbitrarily. Unlike ordinary trees, ordinary trees have at least one node, while binary trees can have zero nodes; ordinary trees have no limit on the maximum degree of nodes, while binary tree nodes have a maximum degree of 2; ordinary tree nodes have no left-right order, while binary tree nodes do have left-right order. — From Wikipedia - Binary tree
Binary trees are very important data structures. Their unique structure gives them excellent performance in searching and processing data.
Binary Tree Traversal
Level Order Traversal (Breadth-First Search)
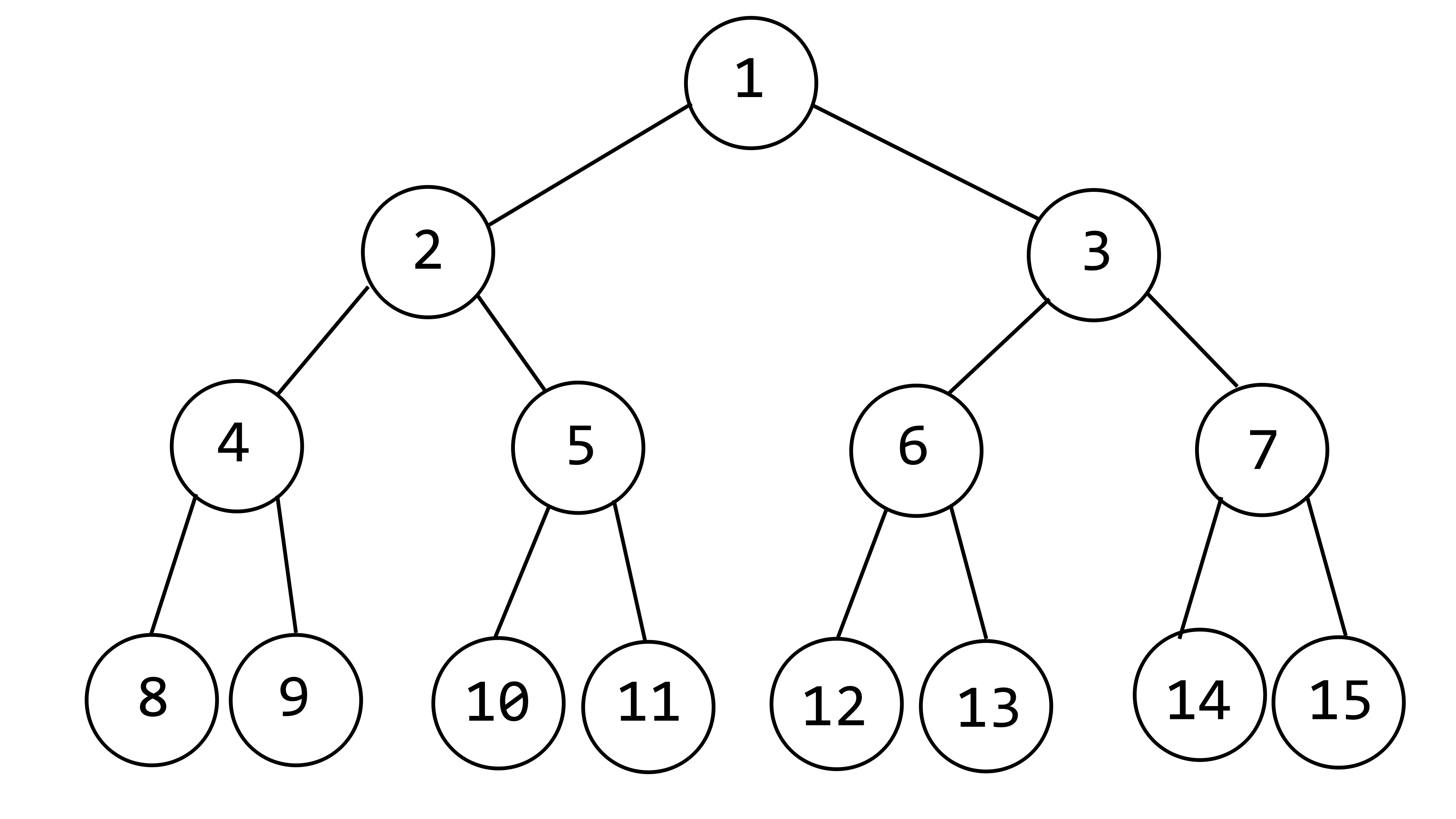
As the name suggests, nodes are traversed from top to bottom, left to right.
Using the image above as an example, the traversal order is 1~15.
This method is called Breadth-First Search (BFS).
Recursive Traversal (Depth-First Search)
The blogger believes that recursive traversal of binary trees is the most wonderful part. Understanding its three recursive traversal methods gives a glimpse of the structural beauty of binary trees.
For a binary tree T, its pre-order, in-order, and post-order traversals can be recursively defined as follows:
- PreOrder(T) = T’s root node + PreOrder(T’s left subtree) + PreOrder(T’s right subtree)
- InOrder(T) = InOrder(T’s left subtree) + T’s root node + InOrder(T’s right subtree)
- PostOrder(T) = PostOrder(T’s left subtree) + PostOrder(T’s right subtree) + T’s root node
These three traversals all belong to recursive traversal, or Depth-First Search (DFS), because it always prioritizes going deeper. — From Liu Rujia “Algorithm Competition Introduction Classic (2nd Edition)”
Still using the image above, let’s talk about how to traverse recursively:
To traverse the entire binary tree, first treat 1, 2, 3 as a small binary tree to traverse, where 1 is the root and 2, 3 are nodes. When traversing nodes 2 or 3, treat 2, 4, 5 or 3, 6, 7 as small binary trees respectively, and so on. The specific traversal order depends on the traversal method.
Is it simple? Before looking at the answers below, try writing out the order for these three traversal methods yourself.
Note: “Root” — root node, “Left” — left subtree, “Right” — right subtree Still using the image above:
Pre-order Traversal
Order: Root --> Left --> Right
1 2 4 8 9 5 10 11 3 6 12 13 7 14 15
In-order Traversal
Order: Left --> Root --> Right
8 4 9 2 10 5 11 1 12 6 13 3 14 7 15
Post-order Traversal
Order: Left --> Right --> Root
8 9 4 10 11 5 2 12 13 6 14 15 7 3 1
Example: Deriving Pre-order Traversal
Given a binary tree’s in-order and post-order traversals, how to reconstruct the tree to write its pre-order traversal?
Using Python-style pseudocode, [] represents list (ordered), {} represents set (unordered).
InOrder = [7, 8, 11, 3, 5, 16, 12, 18]
PostOrder = [8, 3, 11, 7, 16, 18, 12, 5]
From the characteristics of post-order traversal, the last element 5 is the root. Find 5 in the in-order traversal, treat {7, 8, 11, 3} as the left subtree and {16, 12, 18} as the right subtree, and construct a binary tree:
5
/ \
{7, 8, 11, 3} {16, 12, 18}
Next, look at post-order traversal, find roots in [8, 3, 11, 7] and [16, 18, 12] respectively, and similarly construct small binary trees:
5
/ \
7 12
\ / \
{8, 11, 3} 16 18
Final step:
5
/ \
7 12
\ / \
11 16 18
/\
8 3
So we can get its pre-order traversal:
PreOrder = [5, 7, 11, 8, 3, 12, 16, 18]
Example Problems
Deriving Pre-order Traversal
This is the code implementation of the example above. Similar problems: Lia out playing, and reference answer
pre_order.py
pre_order, in_order, post_order = [], '', ''
def read_list():
global pre_order, in_order, post_order
in_order = input()
post_order = input()
pre_order = []
in_order = list(map(int, in_order.split()))
post_order = list(map(int, post_order.split()))
def build_pre(in_order, post_order):
"""Recursively construct binary tree pre-order traversal"""
global pre_order
# Visually see the recursion steps
print("in_order = ", in_order)
print("post_order = ", post_order)
print("pre_order = ", pre_order, "\n")
root = post_order[-1]
pre_order.append(root) # For pre-order traversal, just record the root when constructing subtrees
root_in_order = in_order.index(root)
in_left = in_order[:root_in_order]
in_right = in_order[root_in_order+1 : len(in_order)]
post_left = post_order[:len(in_left)]
post_right = post_order[len(in_left) : -1]
if len(post_left):
build_pre(in_left, post_left)
if len(post_right):
build_pre(in_right, post_right)
while 1:
try:
read_list()
except:
break
build_pre(in_order, post_order)
print("PreOrder: ", end='')
for i in pre_order:
print(i, end=' ')
print("\n")
Output Example:
7 8 11 3 5 16 12 18 # In-order
8 3 11 7 16 18 12 5 # Post-order
in_order = [7, 8, 11, 3, 5, 16, 12, 18]
post_order = [8, 3, 11, 7, 16, 18, 12, 5]
pre_order = [] # Read data
in_order = [7, 8, 11, 3]
post_order = [8, 3, 11, 7]
pre_order = [5] # First recursion step, add root node 5
in_order = [8, 11, 3]
post_order = [8, 3, 11]
pre_order = [5, 7] # Second recursion step, add root node 7
in_order = [8]
post_order = [8]
pre_order = [5, 7, 11]
in_order = [3]
post_order = [3]
pre_order = [5, 7, 11, 8]
in_order = [16, 12, 18]
post_order = [16, 18, 12]
pre_order = [5, 7, 11, 8, 3]
in_order = [16]
post_order = [16]
pre_order = [5, 7, 11, 8, 3, 12]
in_order = [18]
post_order = [18]
pre_order = [5, 7, 11, 8, 3, 12, 16]
PreOrder: 5 7 11 8 3 12 16 18
Level Order Traversal (Trees on the level, UVa 122)
Problem:
Analysis: Use dynamic structure to build tree. Code from the “Algorithm Competition Introduction Classic”:
trees_on_the_level.cpp
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int maxn = 256 + 10;
// Node type
struct Node
{
bool have_value;
int v; // Node value
Node *left, *right;
Node() : have_value(false), left(NULL), right(NULL){} // Constructor
};
Node *root; // Root of binary tree
Node *newnode() { return new Node(); }
bool failed;
void addnode(int v, char *s)
{
int n = strlen(s);
Node *u = root; // Traverse from root
for (int i = 0; i < n; i++)
{
if (s[i] == 'L')
{
if (u->left == NULL) u->left = newnode(); // Node doesn't exist, create new node
u = u->left; // Move left
}
else if (s[i] == 'R')
{
if (u->right == NULL) u->right = newnode();
u = u->right;
}
}
if (u->have_value) failed = true;
u->v = v;
u->have_value = true; // Don't forget to mark
}
void remove_tree(Node *u)
{
if (u == NULL) return; // Early check is safer
remove_tree(u->left); // Recursively free left subtree space
remove_tree(u->right); // Recursively free right subtree space
delete u; // Call destructor and free node's memory
}
char s[maxn];
bool read_input()
{
failed = false;
remove_tree(root); // Free previous tree's memory
root = newnode();
for (;;)
{
if (scanf("%s", s) != 1) return false;
if (!strcmp(s, "()")) break;
int v;
sscanf(&s[1], "%d", &v);
addnode(v, strchr(s, ',') + 1);
}
return true;
}
bool bfs(vector<int> &ans) // Breadth-First Search
{
queue<Node*> q;
ans.clear();
q.push(root); // Initially only root
while (!q.empty())
{
Node *u = q.front(); q.pop();
if(!u->have_value) return false; // Some node not assigned, input error
ans.push_back(u->v); // Add to output sequence
if (u->left != NULL) q.push(u->left); // Add left child to queue if exists
if (u->right != NULL) q.push(u->right); // Add right child to queue if exists
}
return true; // Input correct
}
int main() {
vector<int> ans;
while(read_input())
{
if(!bfs(ans)) failed = 1;
if(failed) printf("not complete\n");
else
{
for(int i = 0; i < ans.size(); i++)
{
if(i != 0) printf(" ");
printf("%d", ans[i]);
}
printf("\n");
}
}
return 0;
}
Summary: Use struct + pointer to implement binary tree. Of course, array + index can also be used, but it depends on the situation.
Recursive Traversal of Binary Trees (Trees, UVa 548)
Problem:
Analysis: Given in-order and post-order traversals of a binary tree, derive pre-order traversal. Still from the classic book:
trees.cpp
#include <iostream>
#include <string>
#include <sstream>
#include <algorithm>
using namespace std;
const int maxv = 10000 + 10;
int in_order[maxv], post_order[maxv], lch[maxv], rch[maxv];
int n;
// Since all node weights are unique positive integers, use weights as node indices directly
bool read_list(int *a)
{
string line;
if (!getline(cin, line)) return false;
stringstream ss(line);
n = 0;
int x;
while (ss >> x) a[n++] = x;
return n > 0;
}
// Build binary tree from in_order[L1..R1] and post_order[L2..R2], return tree root
int build(int L1, int R1, int L2, int R2)
{
if (L1 > R1) return 0; // Empty tree
int root = post_order[R2];
int p = L1;
while (in_order[p] != root) p++;
int cnt = p - L1; // Number of nodes in left subtree
lch[root] = build(L1, p-1, L2, L2+cnt-1);
rch[root] = build(p+1, R1, L2+cnt, R2-1);
return root;
}
int best, best_sum; // Current best solution and corresponding weight sum
void dfs(int u, int sum) // Depth First Search
{
sum += u;
if (!lch[u] && !rch[u]) // Leaf
{
if (sum < best_sum || (sum == best_sum && u < best))
{
{ best = u; best_sum = sum; }
}
if (lch[u]) dfs(lch[u], sum);
if (rch[u]) dfs(rch[u], sum);
}
}
int main()
{
while (read_list(in_order))
{
read_list(post_order);
build(0, n-1, 0, n-1);
best_sum = 1000000000;
dfs(post_order[n-1], 0);
cout << best << "\n";
}
return 0;
}
Summary: The difficulty lies in understanding how to use arrays lch and rch to store left and right subtrees of nodes and the tree-building process. It’s recommended to draw diagrams to help understanding.
Balance Scale (Not so Mobile, UVa 839)
Problem: PDF Analysis: Recursively defined binary tree. Still from the classic book, the code is quite concise and clever, worth learning:
not_so_mobile.cpp
#include <iostream>
using namespace std;
// Input a sub-balance, return if it's balanced, parameter W modified to total weight
bool solve(int &W)
{
int W1, D1, W2, D2;
bool b1 = true, b2 = true;
cin >> W1 >> D1 >> W2 >> D2;
if (!W1) b1 = solve(W1);
if (!W2) b2 = solve(W2);
W = W1 + W2;
return b1 && b2 && (W1 * D1 == W2 * D2); // b1: left, b2: right
}
int main()
{
int T, W;
cin >> T;
while (T--)
{
if (solve(W)) cout << "YES\n"; else cout << "NO\n";
if (T) cout << "\n";
}
return 0;
}
not_so_mobile.py
def solve(W):
b1, b2 = True, True
W1, D1, W2, D2 = map(int, input().split())
if W1 == 0:
b1 = solve(W1)
if W2 == 0:
b2 = solve(W2)
W = W1 + W2
return b1 and b2 and (W1*D1 == W2*D2)
W = 0
T = int(input())
while T > 0:
T -= 1
print("YES") if solve(W) else print("No")
if T: print("\n")
The Python version seems more readable (
Python Class Implementation of Binary Tree
Object-oriented programming is really interesting. Building a fully functional class from scratch has the same excitement as building an automated farm in Minecraft (
tree.py
class Node(object):
"""Node class"""
def __init__(self, data=None, left_child=None, right_child=None):
self.data = data
self.left_child = left_child
self.right_child = right_child
class Tree(object):
def __init__(self):
self.root = Node()
def rec_pre_order(self, node=None):
"""Recursive pre-order traversal"""
if node:
print(node.data, end=" ")
self.rec_pre_order(node.left_child)
self.rec_pre_order(node.right_child)
def pre_order(self):
"""Non-recursive pre-order traversal"""
if self.root:
ls = [self.root]
while ls:
node = ls.pop()
print(node.data, end=" ")
if node.right_child:
ls.append(node.right_child)
if node.left_child:
ls.append(node.left_child)
def pre_order2(self):
"""Non-recursive pre-order traversal"""
stack = []
node = self.root
while node or stack:
while node:
print(node.data, end=" ")
stack.append(node)
node = node.left_child
if stack:
node = stack.pop()
node = node.right_child
def rec_in_order(self, node):
"""Recursive in-order traversal"""
if node:
self.rec_in_order(node.left_child)
print(node.data, end=" ")
self.rec_in_order(node.right_child)
def in_order(self):
"""Non-recursive in-order traversal"""
ls = []
node = self.root
while node or len(ls):
while node:
ls.append(node)
node = node.left_child
if len(ls):
node = ls.pop()
print(node.data, end=" ")
node = node.right_child
def in_order2(self):
"""Non-recursive in-order traversal"""
stack = []
node = self.root
while node:
while node:
if node.right_child:
stack.append(node.right_child)
stack.append(node)
node = node.left_child
node = stack.pop()
while stack and (not node.right_child):
print(node.data, end=" ")
node = stack.pop()
print(node.data, end=" ")
if stack:
node = stack.pop()
else:
node = None
def rec_post_order(self, node):
"""Recursive post-order traversal"""
if node:
self.rec_post_order(node.left_child)
self.rec_post_order(node.right_child)
print(node.data, end=" ")
def post_order(self, node):
"""Non-recursive post-order traversal"""
q = node
ls = []
while node:
while node.left_child:
ls.append(node)
node = node.left_child
while node and (node.right_child is None or node.right_child == q):
print(node.data, end=" ")
q = node
if not ls:
return
node = ls.pop()
ls.append(node)
node = node.right_child
def get_depth(self):
"""Calculate tree depth, recursive left and right nodes, take larger depth"""
def _depth(node):
if not node:
return 0
else:
left_depth = _depth(node.left_child)
right_depth = _depth(node.right_child)
if left_depth > right_depth:
return left_depth + 1
else:
return right_depth + 1
return _depth(self.root)
def get_leaves(self, node):
"""Recursively output all leaf nodes"""
if node:
if not node.left_child and not node.right_child:
print(node.data, end=" ")
else:
self.get_leaves(node.left_child)
self.get_leaves(node.right_child)
if __name__ == '__main__':
tree = Tree()
tree.root = Node('A')
tree.root.left_child = Node('B')
tree.root.right_child = Node('C')
tree.root.left_child.left_child = Node('D')
tree.root.left_child.right_child = Node('E')
tree.root.left_child.right_child.right_child = Node('F')
tree.root.left_child.left_child.right_child = Node('G')
print("""
A
|
-------------
| |
B C
|
-------------
| |
D E
| |
------- -------
| | | |
(None) G (None) F
""")
print("#Pre-order Traversal")
print("Recursive:")
tree.rec_pre_order(tree.root)
print("\nNon-recursive 1:")
tree.pre_order()
print("\nNon-recursive 2:")
tree.pre_order2()
print("\n\n#In-order Traversal")
print("Recursive:")
tree.rec_in_order(tree.root)
print("\nNon-recursive 1:")
tree.in_order()
print("\nNon-recursive 2:")
tree.in_order2()
print("\n\n#Post-order Traversal")
print("Recursive:")
tree.rec_post_order(tree.root)
print("\nNon-recursive:")
tree.post_order(tree.root)
print("\n\nBinary tree depth:", tree.get_depth())
print("\nLeaf nodes:", end="")
tree.get_leaves(tree.root)
Binary Search Tree
(I’ll leave this for later updates)

References
- Wikipedia - Binary tree
- Liu Rujia “Algorithm Competition Introduction Classic (2nd Edition)”